This entry outlines the role of the law of non-contradiction (LNC) as the foremost among the first (indemonstrable) principles of Aristotelian philosophy and its heirs, and depicts the relation between LNC and LEM (the law of excluded middle) in establishing the nature of contradictory and contrary opposition. §1 presents the classical treatment of LNC as an axiom in Aristotle's “First Philosophy” and reviews the status of contradictory and contrary opposition as schematized on the Square of Opposition. §2 explores in further detail the possible characterizations of LNC and LEM, including the relevance of future contingent statements in which LEM (but not LNC) is sometimes held to fail. In §3 I briefly discuss the mismatch between the representation of contradictory negation as a propositional operator and its varied realization within natural language. §4 deals with several challenges to LNC within Western philosophy, including the paradoxes, and the relation between systems with truth-value gaps (violating LEM) and those with truth-value gluts (violating LNC). Finally, in §5, the tetralemma of Buddhist logic is discussed within the context of gaps and gluts; it is argued that apparent violations of LNC in this tradition and others can in be attributed to either differing viewpoints of evaluation (as foreseen by Aristotle) or to intervening modal and epistemic operators.
The twin foundations of Aristotle's logic are the law of non-contradiction (LNC) (also called the law of contradiction) and the law of excluded middle (LEM). In Metaphysics Book Gamma, LNC—“the most certain of all principles”—is defined as follows:
It is impossible that the same thing can at the same time both belong and not belong to the same object and in the same respect, and all other specifications that might be made, let them be added to meet local objections (1005b19-23).
For Aristotle, the status of LNC as a first, indemonstrable principle is obvious. Those who stubbornly demand a proof of LNC simply “lack education”: since “a demonstration of everything is impossible”, resulting in infinite regress, at least some principles must be taken as primitive axiomata rather than derived from other propositions—and what principle more merits this status than LNC? (1006a6-12). In first philosophy, as in mathematics, an axiom is both indemonstrable and indispensable; without LNC, “a is F” and “a is not F” are indistinguishable and no argumentation is possible. While Sophists and “even many physicists” may claim that it is possible for the same thing to be and not to be at the same time and in the same respect, such a position self-destructs “if only our opponent says something”, since as soon as he opens his mouth to make an assertion, any assertion, he must accept LNC. But what if he does not open his mouth? Against such an individual “it is ridiculous to seek an argument” for he is no more than a vegetable (1006a1-15).
The role of LNC as the basic, indemonstrable “first principle” is affirmed by Leibniz, for whom LNC is taken as interdefinable with another of Aristotle's axiomata, the Law of Identity: “Nothing should be taken as first principles but experiences and the axiom of identity or (what is the same thing) contradiction, which is primitive, since otherwise there would be no difference between truth and falsehood, and all investigation would cease at once, if to say yes or no were a matter of indifference” (Leibniz 1696/Langley 1916: 13-14). For Leibniz, everybody—even “barbarians”—must tacitly assume LNC as part of innate knowledge implicitly called upon at every moment, thus demonstrating the insufficiency of Locke's empiricism (ibid., 77). [1]
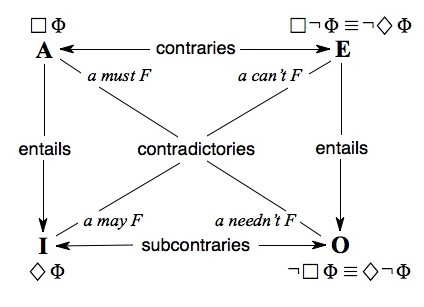
In accounting for the incompatibility of truth and falsity, LNC lies at the heart of the theory of opposition, governing both contradictories and contraries. (See traditional square of opposition.) Contradictory opposites (“She is sitting”/“She is not sitting”) are mutually exhaustive as well as mutually inconsistent; one member of the pair must be true and the other false. As it was put by the medievals, contradictory opposites divide the true and the false between them; for Aristotle, this is the primary form of opposition. [2] Contrary opposites (“He is happy”/“He is sad”) are mutually inconsistent but not necessarily exhaustive; they may be simultaneously false, though not simultaneously true. LNC applies to both forms of opposition in that neither contradictories nor contraries may belong to the same object at the same time and in the same respect (Metaphysics 1011b17-19). What distinguishes the two forms of opposition is a second indemonstrable principle, the law of excluded middle (LEM): “Of any one subject, one thing must be either asserted or denied” (Metaphysics 1011b24). Both laws pertain to contradictories, as in a paired affirmation (“S is P”) and denial (“S isn't P”): the negation is true whenever the affirmation is false, and the affirmation is true when the negation is false. Thus, a corresponding affirmation and negation cannot both be true, by LNC, but neither can they both be false, by LEM. But while LNC applies both to contradictory and contrary oppositions, LEM holds only for contradictories: “Nothing can exist between two contradictories, but something may exist between contraries” (Metaphysics 1055b2): a dog cannot be both black and white, but it may be neither.
As Aristotle explains in the Categories, the opposition between contradictories— “statements opposed to each other as affirmation and negation”—is defined in two ways. First, unlike contrariety, contradiction is restricted to statements or propositions; terms are never related as contradictories. Second, “in this case, and in this case only, it is necessary for the one to be true and the other false” (13b2-3).
Opposition between terms cannot be contradictory in nature, both because only statements (subject-predicate combinations) can be true or false (Categories 13b3-12) and because any two terms may simultaneously fail to apply to a given subject. [3] But two statements may be members of either a contradictory or a contrary opposition. Such statements may be simultaneously false, although (as with contradictories) they may not be simultaneously true. The most striking aspect of the exposition for a modern reader lies in Aristotle's selection of illustrative material. Rather than choosing an uncontroversial example involving mediate contraries, those allowing an unexcluded middle (e.g. “This dog is white”/“This dog is black”; “Socrates is good”/“Socrates is bad”), Aristotle offers a pair of sentences containing immediate contraries, “Socrates is sick”/“Socrates is well”. These propositions may both be false, even though every person is either ill or well: “For if Socrates exists, one will be true and the other false, but if he does not exist, both will be false; for neither ‘Socrates is sick’ nor ‘Socrates is well’ will be true, if Socrates does not exist at all” (13b17-19). But given a corresponding affirmation and negation, one will always be true and the other false; the negation “Socrates is not sick” is true whether the philosopher is healthy or non-existent: “for if he does not exist, ‘he is sick’ is false but ‘he is not sick’ true” (13b26-35).
Members of a canonical pair of contradictories are formally identical except for the negative particle:
An affirmation is a statement affirming something of something, a negation is a statement denying something of something…It is clear that for every affirmation there is an opposite negation, and for every negation there is an opposite affirmation…Let us call an affirmation and a negation which are opposite a contradiction (De Interpretatione 17a25-35).
But this criterion, satisfied simply enough in the case of singular expressions, must be recast in the case of quantified expressions, both those which “signify universally” (“every man”, “no man”) and those which do not (“some man”, “not every man”).
For such cases, Aristotle shifts from a formal to a semantically based criterion of opposition (17b16-25). The A/O pair (“Every man is white”, “Not every man is white”) and I/E pair (“Some man is white”, “No man is white”) are contradictories because in any state of affairs one member of each pair must be true and the other false. (See traditional square of opposition.) Similarly, the A/E pair—“Every man is just”, “No man is just”—are contraries, since these cannot be true together. The contradictories of two contraries (“Not every man is just”, “Some man is just”) can be simultaneously true with reference to the same subject; (17b23-25). The last opposition of I and O statements, later to be dubbed subcontraries because they appear below the contraries on the traditional square, is a peculiar opposition indeed; Aristotle elsewhere (Prior Analytics 63b21-30) sees I and O as “only verbally opposed”, given the mutual consistency of “Some Greeks are bald” and “Some Greeks aren't bald”.
The same relations obtain for modal propositions, those involving binary connectives like “and” and “or”, quantificational adverbs, and a range of other expressions that can be mapped in analogous ways (see Horn 1989). Thus for example we have the following modal square, based on De Interpretatione 21b10ff. and Prior Analytics 32a18-28:

In the twelfth century, Peter of Spain (1972: 7) offers a particularly elegant formulation in his Tractatus; it will be seen that these apply to the modal propositions in (1) as well as to the quantificational statements in the original square:
The law of excluded middle, LEM, is another of Aristotle's first principles, if perhaps not as first a principle as LNC. Just as Heraclitus's anti-LNC position, “that everything is and is not, seems to make everything true”, so too Anaxagoras's anti-LEM stance, “that an intermediate exists between two contradictories, makes everything false” (Metaphysics 1012a25-29). Of any two contradictories, LEM requires that one must be true and the other false (De Interpretatione 18a31)—or does it? In a passage that has launched a thousand treatises, Aristotle (De Interpretatione, Chapter 9) addresses the difficulties posed by apparently contradictory contingent statements about future events, e.g. (2a,b).
(2a) There will be a sea-battle tomorrow.
(2b) There will not be a sea-battle tomorrow.
Clearly, (2a) and (2b) cannot both be true; LNC applies to future contingents as straightforwardly as to any other pair of contradictories. But what of LEM? Here is where the difficulties begin, culminating in the passage with which Aristotle concludes and (apparently) summarizes his account:
It is necessary for there to be or not to be a sea-battle tomorrow; but it not necessary for a sea-battle to take place tomorrow, nor for one not to take place—though it is necessary for one to take place or not to take place. So, since statements are true according to how the actual things are, it is clear that wherever these are such as to allow of contraries as chance has it, the same necessarily holds for the contradictories also. This happens with things that are not always so or are not always not so. With these it is necessary for one or the other of the contradictories to be true or false—not, however, this one or that one, but as chance has it; or for one to be true rather than the other, yet not already true or false. Clearly, then it is not necessary that of every affirmation and opposite negation one should be true and the other false. For what holds for things that are does not hold for things that are not but may possibly be or not be; with these it is as we have said (De Interpretatione 19a30-b4).
Unfortunately, given the systematic ambiguity and textual variations in the Greek text, the difficulty of telling when Aristotle is speaking with his own voice or characterizing an opponent's argument, and the lack of formal devices for the essential scopal distinctions at issue, it has never been clear exactly just what has been said here and in the chapter more generally. Some, including Boethius and Lukasiewicz, have seen in this text an argument for rejecting LEM for future contingent statements, which are therefore to be assigned a non-classical value (e.g. “Indeterminate”) or no truth-value at all. [4] Their reasoning is based in part on the premise that the alternative position seems to require the acceptance of determinism. Others, however, read Aristotle as rejecting not simple bivalence for future contingents but rather determinacy itself. This interpretive tradition, endorsed by al-Fârâbi, Saint Thomas, and Ockham, is crystallized in this passage from Abelard's Dialectica (210-22) cited by Kneale and Kneale (1962: 214):
No proposition de contingenti futuro can be determinately true or determinately false…, but this is not to say that no such proposition can be true or false. On the contrary, any such proposition is true if the outcome is to be true as it states, even though this is unknown to us.
Even if we accept the view that Aristotle is uncomfortable with assigning truth (or falsity) to (2a) and (2b), their disjunction in (3a) is clearly seen as true, and indeed as necessarily true. But the modal operator must be taken to apply to the disjunction as a whole as in (3b) and not to each disjunct as in (3c).
(3a) Either there will be or there will not be a sea-battle tomorrow.
(3b) □ (Φ ∨ ¬Φ)
(3c) □ Φ ∨ □ ¬Φ
For Aristotle, LNC is understood not as the principle of propositional logic that no statement can be true simultaneously with its negation, but as a prima facie rejection of the possibility that any predicate F could both hold and not hold of a given subject (at the same time, and in the same respect). A full rendering of the version of LNC appearing at Metaphysics 1006b33-34—“It is not possible to truly say at the same time of a thing that it is a man and that it is not a man”—would require a representation involving operators for modality and truth and allowing quantification over times. [5] In the same way, LEM is not actually the principle that every statement is either true or has a true negation, but the law that for any predicate F and any entity x, x either is F or isn't F.
But these conceptualizations of LNC and LEM must be generalized, since the principle that it is impossible for a to be F and not to be F will not apply to statements of arbitrary complexity. We can translate the Aristotelian language, with some loss of faithfulness, into the standard modern versions in (4a,b) respectively, ignoring the understood modal and temporal modifications:
(4a) LNC: ¬(Φ & ¬Φ)
(4b) LEM: Φ ∨ ¬Φ
Taking LNC and LEM together, we obtain the result that exactly one proposition of the pair is true and exactly one is false, where ¬ represents contradictory negation.
Alternatively, the laws can be recast semantically as in (5), again setting aside the usual qualifications:
(5a) LNC: No proposition may be simultaneously true and false.
(5b) LEM: Every proposition must be either true or false.
Not every natural language negation is a contradictory operator, or even a logical operator. A statement may be rejected as false, as unwarranted, or as inappropriate—misleading, badly pronounced, wrongly focused, likely to induce unwanted implicatures or presuppositions, overly or insufficiently formal. Only in the first of these cases, as a toggle between truth and falsity, is it clear that contradictory negation is involved (Horn 1989, Smiley 1993). But is every contradictory negation sentential?
Within propositional logic, contradictory negation is a self-annihilating operator: ¬(¬Φ) is equivalent to Φ. This is explicitly recognized in the proto-Fregean Stoic logic of Alexander of Aphrodisias: “‘Not: not: it is day’ differs from ‘it is day’ only in manner of speech” (Mates 1953: 126). The Stoics' apophatikon directly prefigures the iterating and self-cancelling propositional negation of Frege and Russell. As Frege puts it (1919: 130), “Wrapping up a thought in double negation does not alter its truth value.” The corresponding linguistic principle is expressed in the grammarians' bromide, “Duplex negatio affirmat.”
Not all systems of propositional logic accept a biconditional law of double negation (LDN), ¬(¬Φ) ≡ Φ. In particular, LDN, along with LEM, is not valid for the Intuitionists, who reject ¬(¬Φ) → Φ while accepting its converse, Φ → ¬(¬Φ). But the very possibility of applying negation to a negated statement presupposes the analysis of contradictory negation as an iterative operator (one capable of applying to its own output), or as a function whose domain is identical to its range. Within the categorical term-based logic of Aristotle and his Peripatetic successors, every statement—whether singular or general—is of subject-predicate form. Contradictory negation is not a one-place operator taking propositions into propositions, but rather a mode of predication, a way of combining subjects with predicates: a given predicate can be either affirmed or denied of a given subject. Unlike the apophatikon or propositional negation connective introduced by the Stoics and formalized in Fregean and Russellian logic, Aristotelian predicate denial, while toggling truth and falsity and yielding the semantics of contradictory opposition, does not apply to its own output and hence does not syntactically iterate. In this respect, predicate denial both anticipates the form of negation in Montague Grammar and provides a more plausible representation of contradictory negation in natural language, whether Ancient Greek or English, where reflexes of the iterating one-place connective of the Stoics and Fregeans (“Not: not: the sun is shining”) are hard to find outside of artificial constructs like the “it is not the case” construction (Horn 1989, §7.2). In a given natural language, contradictory negation may be expressed as a particle associated with a copula or a verb, as an inflected auxiliary verb, as a verb of negation, or as a negative suffix or prefix.
In addition, there is a widespread pragmatically motivated tendency for a formal or semantic contradictory negation to be strengthened to a contrary through such processes as litotes (“I don't like prunes” conveying that I dislike prunes) and so-called negative raising (“I don't think that Φ” conveying “I think that ¬Φ”); similarly, the adjective-forming prefixal negation in such words as “unhappy” or “unfair” is understood as a contrary rather than contradictory (not-Adj) of its base. These phenomena have been much discussed by rhetoricians, logicians, and linguists (see Horn 1989: Chap. 5).
In addition to predicate denial, in which a predicate F is denied of a subject a, Aristotelian logic allows for narrow-scope predicate term negation, in which a negative predicate not-F is affirmed of a. The relation of predicate denial and predicate term negation to a simple affirmative proposition can be schematized on a generalized square of opposition (De Interpretatione 19b19-30, Prior Analytics Chapter 46):
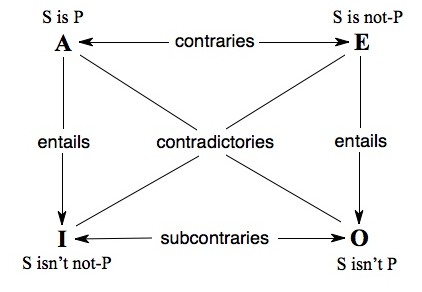
If Socrates doesn't exist, “Socrates is wise” (A) and its contrary “Socrates is not-wise” (E) are both automatically false (since nothing—positive or negative—can be truly affirmed of a non-existent subject), while their respective contradictories “Socrates is not wise” (O) and “Socrates is not not-wise” (I) are both true. Similarly, for any object x, either x is red or x is not red—but x may be neither red nor not-red; if, for instance, x is a unicorn or a prime number.
While Russell (1905), without acknowledgment, echoed Aristotle's ambiguist analysis of negation as either contradictory (“external”) or contrary (“internal”), by virtue of the two logical forms assigned to “The king of France is not bald” (see descriptions), such propositionalized accounts are bought at a cost of naturalness, as singular sentences of subject-predicate grammatical form are assigned the logical form of an existentially quantified conjunction and as names are transmuted into predicates.
In addition to the future contingent statements discussed, vacuous subjects like those in (7a,b) have sometimes been taken to yield a violation of LEM through the emergence of a truth-value gap.
(7a) is bald.
(7b) isn't bald.
While Aristotle would see a republican France as rendering (7a) false and (7b) automatically true, Frege (1892) and Strawson (1950) reject the notion that either of these sentences can be used to make a true or false assertion. Instead, both statements presuppose the existence of a referent for the singular term; if the presupposition fails, so does the possibility of classical truth assignment. Note, however, that such analyses present a challenge to LEM only if (7b) is taken as the true contradictory of (7a), an assumption not universally shared. Russell, for example, allows for one reading of (7b) on which it is, like (7a), false in the absence of a referent for the subject term.
In those systems that do embrace truth value gaps (Strawson, arguably Frege) or non-classically-valued systems (Lukasiewicz, Bochvar, Kleene), some sentences or statements are not assigned a (classical) truth value; in Strawson's famous dictum, the question of the truth value of “The king of France is wise”, in a world in which France is a republic, simply fails to arise. The negative form of such vacuous statements, e.g. “The king of France is not wise”, is similarly neither true nor false. This amounts to a rejection of LEM, as noted by Russell 1905. In addition to vacuous singular expressions, gap-based analyses have been proposed for future contingents (following one reading of Aristotle's exposition of the sea-battle; cf. §2 above) and category mistakes (e.g. “The number 7 likes/doesn't like to dance”).
While LNC has traditionally remained more sacrosanct, reflecting its position as the primus inter pares of the indemonstrables, transgressing this final taboo has become increasingly alluring in recent years. The move here involves embracing not gaps but truth value gluts, cases in which a given sentence and its negation are taken to be both true, or alternatively cases in which a sentence may be assigned more than one (classical) truth value, i.e. both True and False. Parsons (1990) observes that the two non-classical theories are provably logically equivalent, as gluts arise within one class of theories precisely where gaps do in the other. Further, dialetheism escapes the charge of incoherence by avoiding the logical armageddon of Ex Contradictione Quodlibet, the inference in (8):
(8) p, ¬p
_____
∴q
Far from reduced to the silence of a vegetable, as Aristotle ordained, the proponents of true contradictions, including self-avowed dialetheists like Sylvan (né Routley) and Priest have been eloquent.
Is the status of Aristotle's “first principle” as obvious as he believed? Adherents of the dialetheist view that there are true contradictories (Priest 1987, 1998, 2002; see also dialetheism and paraconsistent logic) would answer firmly in the negative. [6] In the Western tradition, the countenancing of true contradictions is typically—although not exclusively—motivated on the basis of such classic logical paradoxes as “This sentence is not true” and its analogues (the Liar, the Barber, Russell's paradox), each of which is true if and only if it is not true. As Smiley (1993: 19) has remarked, “Dialetheism stands to the classical idea of negation like special relativity to Newtonian mechanics: they agree in the familiar areas but diverge at the margins (notably the paradoxes).”
In addition to the Liar, another locus classicus is the problem of omnipotence as crystallized in the Paradox of the Stone. One begins by granting the basic dilemma, as an evident instance of LEM: either God is omnipotent or God is not omnipotent. With omnipotence, He can do anything, and in particular He can create a stone x so heavy that even He cannot lift it. But then there is something He cannot do, viz. (ex hypothesi) lift x. But this is an instance of LNC: God can lift x and God cannot lift x.
This paradox, and the potential challenge it offers to either LNC or the possibility of omnipotence, has been recognized since Aquinas, who opted for retaining the Aristotelian law by understanding omnipotence as the capacity to do only what is not logically impossible. (Others, including Augustine and Maimonides, have noted that in any case God is “unable” to do what is inconsistent with His nature, e.g. commit sin.) For Descartes, on the other hand, an omnipotent God is by definition capable of any task, even those yielding contradictions. Mavrodes (1963), Kenny, and others have sided with Aquinas in taking omnipotence to extend only to those powers it is possible to possess; Frankfurt (1964), on the other hand, essentially adopt the Cartesian line: Yes, of course God can indeed construct a stone that He cannot lift—and what's more, He can lift it! (See also Savage 1967 for a related solution.)
Within Western philosophy, Hegel has often been depicted as a leading LNC-skeptic, but in fact for Hegel an unresolved contradiction is a sign of error. The contradiction between thesis and antithesis results in Aufhebung, the dialectical resolution or superseding of the contradiction between opposites as a higher-level synthesis that eventually generates its own antithesis. Rather than repudiating LNC, Hegel's dialectic rests upon it. In Marxist theory, too, contradictories do not simply cancel out but are dynamically resolved (aufgehoben) at a higher level in a way that both preserves and supersedes the contradiction, motivating the historical dialectic. (See Horn 1989: §1.3.2.)
For Freud, there is a realm in which LNC is not so much superseded but dissolved. On the primary, infantile level, reflected in dreams and neuroses, there is no not: “‘No’ seems not to exist as far as dreams are concerned. Anything in a dream can mean its contrary” (Freud 1910: 155). When the analysand insists of a dream character “It's not my mother”, the analyst silently translates, “So it is his mother!”
Given Aristotle's observation that “even some physicists” deny LNC and affirm that is indeed possible for the same thing to be and not to be at the same time and in the same respect, he would not have been surprised to learn that quantum mechanics has made such challenges fashionable again. Thus, we have Schrödinger's celebrated cat, placed (within the context of a thought experiment) inside a sealed box along with radioactive material and a vial of poison gas that will be released if that material decays. Given quantum uncertainty, an atom inhabits both states—decayed and non-decayed—simultaneously, rendering the cat (in the absence of an observer outside the system) both alive and dead. Where speculative consensus breaks down is on whether Schrödinger's paradox arises only when the quantum system is isolated from the environment.
Aristotle himself anticipated many of the challenges that have since been raised against LNC. Thus whether it is the ambivalence of Zerlina's “Vorrei e non vorrei”, Strawson's exchange (1952: 7)
—Were you pleased?
—Well, I was and I wasn't.
or the observation of Jainists two millennia ago that “S is P” and “S is not P” can both be true from different standpoints (Raju 1954: 698-701; Balcerowicz 2003), we have ample opportunity to reflect on the foresight of Aristotle's rider: “S is P” and “S is not P” cannot both hold in the same sense, at the same time, and in the same respect.
Outside the Western canon, the brunt of the battle over LNC has been largely borne by the Buddhists, particularly in the exposition by Nâgârjuna of the catuskoti or tetralemma (c. 200 A.D.; cf. Bochenski 1961: Part VI, Raju 1954, Garfield 1995, Tillemans 1999, Garfield & Priest 2002), also known as the four-cornered or fourfold negation. Consider the following four possible truth outcomes for any statement and its (apparent) contradictory:
| (9) (i) | S is P |
| (ii) | S is not P |
| (iii) | S is both P and not-P |
| (iv) | S is neither P nor not-P |
For instances of the positive tetralemma, all four statement types can or must be accepted, e.g.:
Everything is real and not real.
Both real and not real.
Neither real nor not real.
That is Lord Buddha's teaching.
—Mûla-madhyamaka-kârikâ 18:8, quoted in Garfield (1995: 102)
Such cases arise only when we are beyond the realm to which ordinary logic applies, when “the sphere of thought has ceased.” On the other hand, much more use is made of the negative tetralemma, in which all four of the statements in (9) can or must be rejected. Is this tantamount, as it appears, to the renunciation of LEM and LNC, the countenancing of both gaps and gluts, and thus—in Aristotle's view—the overthrow of all bounds of rational argument?
It should first be noted that the axiomatic status of LNC and LEM is as well-established within the logical traditions of India as it is for the Greeks and their epigones. [7] And indeed, Garfield (1995) and Tillemans (1999) convincingly refute the claim that Nâgârjuna was an “irrationalist”. [8] In the first place, if Nâgârjuna simply rejected LNC, there would be no possibility of reductio arguments, which hinge on the establishment of untenable contradictions, yet such arguments are standardly employed in his logic. In fact, he overtly prohibits virodha (contradiction). Crucially, it is only in the realm of the Absolute or Transcendent, where we are contemplating the nature of the ultimate, that contradictions are embraced; in the realm of ordinary reality, LNC operates and classical logic holds. In this sense, the logic of Nâgârjuna and of the Buddhist tradition more generally can be seen not as inconsistent but paraconsistent.
One aspect of the apparent paradox is precisely parallel to that arising with some of the potential counterexamples to the LNC arising in Western thought. In various Buddhist and Jainist systems of thought, the apparent endorsement of Fa & ¬Fa (or, in propositional terms, Φ & ¬Φ) is upon closer examination qualified in precisely the way foreseen by the codicils in Aristotle's statement of the law: “From a certain viewpoint, Φ (e.g. Nirvana exists); from a certain viewpoint, ¬Φ (e.g. Nirvana does not exist).
To further explore the status of truth-value gluts, in which both classical values are simultaneously assigned to a given proposition (e.g. “x is real”), let us consider the analogous cases involving gaps. Recall, for example, the case of future contingents as in (2a,b) above: we need not maintain that “Iraq will become a secular democracy” is neither true nor false when uttered today, but only that neither this statement nor its contradictory “Iraq will not become a secular democracy” is assertable today in the absence of foreknowledge. Similarly for past unknowables, such as (to adapt an example from Quine) the proposition that the number of blades of grass on the Old Campus lawn during the 2005 Yale commencement exercises was odd. This is again more plausibly viewed as unassertable than as truth-valueless, even though its truth-value will never be known. To take a third example, we can argue, with Grice (1989: 80ff.), that a negation outside the scope of a conditional is generally intended as a refusal (or hesitation) to assert “if p then q” rather than as the contradictory negation of a conditional, whose truth value is determined in accord with the standard material equivalence:
(10) ¬(p→q) ≡ (p & ¬q)
Thus, in denying your conditional “If you give her penicillin, she will get better”, I am allowing for the possibility that giving her penicillin might have no effect on her, but I am not predicting that you will administer the penicillin and she will fail to recover. Nor does denying the apothegm (typically though inaccurately attributed to Dostoyevsky or Nietzsche) that if God is dead everything is permitted commit one to the conjoined proposition that God is dead and something is forbidden. As Dummett (1973: 328-30) puts the point, we must distinguish negation outside the scope of a Fregean assertion operator, not (⊢p), from the assertion of a negative proposition, ⊢(not p). The former interpretation “might be taken to be a means of expressing an unwillingness to assert” p, in particular when p is a conditional:
| (11) X: | If it rains, the match will be canceled. |
| Y: | That's not so. (or, I don't think that's the case.) |
Y's contribution here does not constitute a negation of X's content; rather, we can paraphrase Y as conveying (11′a) or (11′b):
(11′a) If it rains, the match won't necessarily be canceled.
(11′b) It may [epistemic] happen that it rains and yet the match is not canceled.
Dummett observes, “We have no negation of the conditional of natural language, that is, no negation of its sense: we have only a form for expressing refusal to assent to its assertion.”
Similarly with disjunction. Consider the exchange in (12) preceding the 2000 election, updated from an example of Grice:
| (12) X: | Bush or Gore will be elected. |
| Y: | That's not so: Bush or Gore or Nader will be elected. |
Y's rejoinder cannot be a contradictory of the content of X's claim, since the (de jure) election of Bush rendered both X's and Y's statements true. Rather, Y objects on the grounds that X is not in an epistemic position to assert the binary disjunction.
Unassertability can be read as the key to the apparent paradox of the catuskoti as well. The venerable text in Majjhima-nikâya 72, relating the teachings of the historical Buddha, offers a precursor for Nâgârjuna's doctrine of the negative tetralemma. Gotama is responding to a monk's question concerning the doctrine of rebirth (quoted in Robinson 1967: 54):
Gotama, where is the monk reborn whose mind is thus freed?
Vaccha, it is not true to say that he is reborn.
Then, Gotama, he is not reborn.
Vaccha, it is not true to say that he is not reborn.
Then, Gotama, he is both reborn and not reborn.
Vaccha, it is not true to say that he is both reborn and not reborn.
Then, Gotama, he is neither reborn nor not reborn.
Vaccha, it is not true to say that he is neither reborn nor not reborn.
Note the form of the translation here, or similarly that of the standard rendering of the negative catuskoti that “it profits not” to assert Φ, to assert ¬Φ, to assert both Φ and ¬Φ, or to assert neither Φ nor ¬Φ: the relevant negation can be taken to operate over an implicit modal, in particular an epistemic or assertability operator. If so, neither LEM nor LNC is directly at stake in the tetralemma: you can have your Aristotle and Buddha too.
We tend to recalibrate apparent violations of LNC as conforming to a version of the law that incorporates the Aristotelian qualifications: a sincere defense of “p and not-p” plausibly involves a change in the context of evaluation or a shift in viewpoint, or alternatively a suppression of modal or epistemic operators. This practice can be seen as an instance of a general methodological principle associated with Davidson and Quine that has come to be called the principle of charity (or, alternately, the principle of rational accommodation): when it is unclear how to interpret another's argument, interpret it in a way that makes the most sense. At the same time, this procedure evokes the standard Gricean mode of explanation: granted the operation of the Cooperative Principle and, more broadly, the premise of Rationality, we reinterpret apparent violations of valid principles or maxims so as to conserve the assumption that one's interlocutor is a rational and cooperative agent. As Aristotle would remind us, no principle is more worthy of conservation than the Law of Non-Contradiction.
[Please contact the author with suggestions.]
I am grateful to an anonymous reader and to Professor Piotr Balcerowicz for very helpful comments.